Carrier and Clock Synchronization in MSK Signals

Minimum Shift Keying (MSK) is a versatile and spectrally efficient digital modulation scheme. On this website, I have previously written a tutorial on MSK in some detail. We saw how MSK is a special case of Continuous-Phase Frequency Shift Keying (CPFSK) which is a special case of Continuous-Phase Modulation (CPM). We also explored how it can also be cast as Offset Quadrature Phase Shift Keying (OQPSK).

In designing a real communication system, the design of modulators and demodulators is the easy part. The main difficulty arises from acquiring synchronization with the incoming signal. Today we investigate the carrier and timing recovery problems in an MKS modem.

Carrier Synchronization

---

In Chapter 7 of Wireless Communications from the Ground Up, we have described in great detail the effect of squaring on a digitally modulated signal. When such a squaring technique is applied to an MSK signal, it produces two strong spectral components at twice the modulation frequencies. Let us find out how.

Reproduce Eq (5) from MSK tutorial first.
\[
s(t) = \cos \left[2\pi F_c t + 2\pi \frac{a_n R_b}{4} t + \Theta_n\right]
\]

Since $R_b=1/T$ and modulation symbols $a_n=\pm 1$, we have
\[
s(t) = \cos \left[2\pi F_c t \pm \frac{\pi t}{2T} + \Theta_n\right]
\]

Let us denote the two frequencies as below.
\begin{align*}
f_+ =& ~F_c+\frac{1}{4T}\\
f_- =& ~F_c-\frac{1}{4T}
\end{align*}

The block diagram of the synchronization circuit is now drawn below.

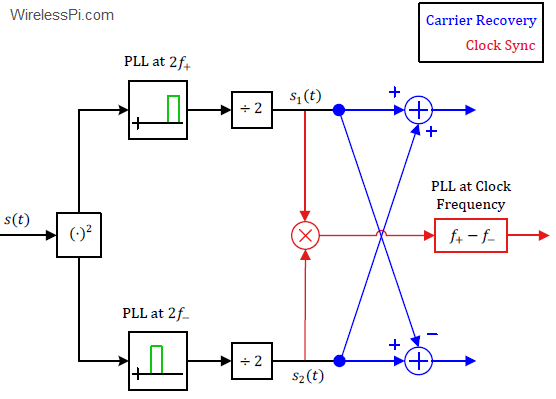
While the above block diagram looks complicated, we now describe how it leads to a straightforward synchronization procedure.

Squaring the signal $s(t)$ above and using the identity $\cos^2\theta = 1/2(1+\cos 2\theta)$ yields
\begin{align*}
s^2(t) =&~ \cos^2 \left[2\pi F_c t \pm \frac{\pi t}{2T} + \Theta_n\right] \\
=& ~\frac{1}{2}+\frac{1}{2}\cos \left[4\pi F_c t \pm \frac{\pi t}{T} + 2\Theta_n\right]\\
=& ~\frac{1}{2}+\frac{1}{2}\cos \left[4\pi F_c t \pm \frac{\pi t}{T}\right]
\end{align*}

because $2\Theta_n=0$ or $2\pi$, see Eq (7) in the same MSK tutorial. Clearly, the two frequencies in the above expression are $2f_+$ and $2f_-$.
\[
s^2(t) = \frac{1}{2}+\frac{1}{2}\cos \left[2\pi \left\{\underbrace{2F_c \pm \frac{1}{2T}}_{2f_+ \text{~and~} 2f_-}\right\}t\right]
\]

Now it is possible to lock onto each frequency through a Phase Locked Loop (PLL) and then divide the frequency of the PLL output by two. Therefore, the division by two shown in the above figure is not for the amplitude, it is for the frequency. The PLLs filter out the DC terms too.
\begin{align*}
s_1(t) =&~ \frac{1}{2}\cos \left(2\pi F_ct ~+ \frac{\pi t}{2T}\right)\\
s_2(t) =&~ \frac{1}{2}\cos \left(2\pi F_ct ~- \frac{\pi t}{2T}\right)
\end{align*}

Using the sum identity of cosines $\cos A + \cos B$ $=$ $2\cos \frac{A+B}{2}\cos \frac{A-B}{2}$, we have the sum in the upper arm.
\[
s_1(t) + s_2(t) = \cos \left(\frac{\pi t}{2T}\right)\cos \left(2\pi F_c t\right)
\]

Similarly, the difference appears in the lower arm as
\[
s_1(t) ~- s_2(t) = \sin \left(\frac{\pi t}{2T}\right)\sin \left(2\pi F_c t\right)
\]

where we have used the identity $\cos A – \cos B$ $=$ $2\sin \frac{A+B}{2}\sin \frac{A-B}{2}$. These are the carrier references required in the upper and lower arms of the O-QPSK version of the MSK demodulator! These are shown through the blue part of the block diagram of the synchronization circuit.

Timing Synchronization

---

To produce the desired clock, let us multiply $s_1(t)$ with $s_2(t)$ and use the identity $2\cos A \cos B$ $=$ $\cos (A-B) + \cos (A+B)$.
\begin{align*}
s_1(t)\cdot s_2(t) =&~ \frac{1}{2}\cos \left(2\pi F_ct + \frac{\pi t}{2T}\right)\cdot \frac{1}{2}\cos \left(2\pi F_ct ~- \frac{\pi t}{2T}\right) \\
\propto&~\cos \frac{\pi t}{T} + \cos 2\pi (2F_c) t
\end{align*}

The double frequency term is filtered out by the timing PLL while the remaining term can be written as
\[
\cos \frac{\pi t}{T} = \cos 2\pi\frac{1}{2T}t
\]

This is the desired clock signal at half the bit rate $1/T$. This is the rate exhibited by the MSK modulated waveform.

Concluding Remarks

---

Some remarks are as below.

• Being a versatile modulation, there are several types of MSK modulators and demodulators. For example, in one particular type of demodulator, the double frequency term in the last equation above can also be used for carrier recovery (although a divided by two operation for frequency is required).
• Due to the squaring operation, there is a $180^\circ$ phase ambiguity. This can be overcome by differential encoding of the data stream and differential decoding at the receive side.