Wireless/SDR Archives | Page 8 of 22

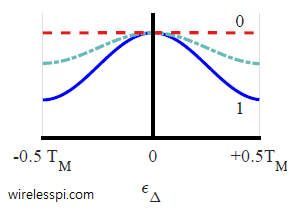
Average trajectory for squared eye diagrams for a binary PAM sequence of 400 symbols shaped with Raised Cosine pulse with excess bandwidths 0, 0.5 and 1

December 24, 2021 Wireless/SDR

Early-Late Bit Synchronizer in Digital Communication

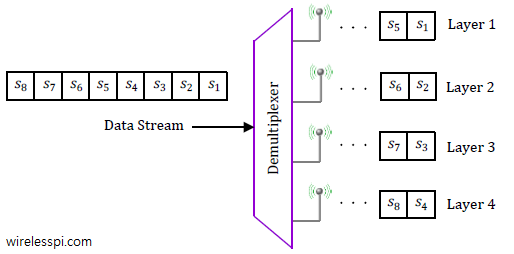
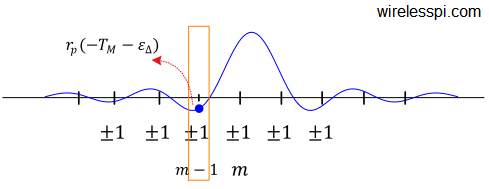
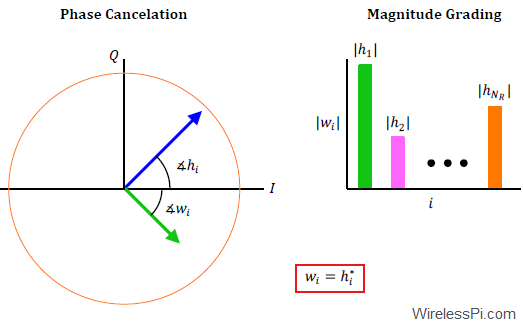
In an article on Phase Locked Loop (PLL) for symbol timing recovery, we described an intuitive view of a maximum likelihood Timing Error Detector (TED). We saw that the timing matched filter is constructed by computing the derivative of the matched filter and consequently its output is the derivative of the input signal. Naturally, this output is more fine-grained and hence accurate when the number of samples/symbol $L$ is large. Here, $L$ must be several times larger than the minimum limit set by the Nyquist theorem. However, in most applications, reducing the complexity of the timing locked loop is far

A V-BLAST architecture for 4 Tx antennas

December 15, 2021 Wireless/SDR

V-BLAST with Successive Interference Cancelation

In the article on Zero-Forcing detector for MIMO receivers, we have seen that the performance of linear detectors is unsatisfactory for actual implementations of conventional MIMO systems. Their main attraction comes from their low computational complexity. To strike a nice balance between performance and complexity, a neat trick is employed by the algorithm known as Successive Interference Cancelation (SIC). The concept was devised by Gerard Foschini from Bell Labs, although it was not a new idea. Successive interference cancelation was already proposed for the detection algorithms in CDMA systems. Again, the fundamental idea was borrowed from decision feedback equalization schemes

October 31, 2020 Wireless/SDR

Mueller and Muller Timing Synchronization Algorithm

Proposed in 1976, Mueller and Muller algorithm is a timing synchronization technique that operates at symbol rate, as opposed to most other synchronization algorithms that require at least 2 samples/symbol such as early-late and Gardner timing error detectors. All of these are feedback techniques that operate within a PLL. Feedforward methods such as digital filter and square timing synchronization are also feasible due to powerful digital signal processing that avoids feedback problems such as hangups. The most confusing thing communication engineers and radio hobbyists find about Mueller and Muller algorithm algorithm is the cross product in its expression: matched filter

November 22, 2021 Wireless/SDR

Maximum Ratio Combining (MRC)

In the discussion on diversity, we described in detail the idea of space diversity through an example of Selection Combining (SC). Maximum Ratio Combining (MRC) is another space diversity scheme that embodies the concept behind generalized beamforming — the main technology in 5G cellular systems. Let us find out how. Setup Consider a wireless link with 2 Tx antenna and 2 (or more) Rx antennas as shown in the figure below. At each symbol time, a data symbol $s$ is transmitted which belongs to a Quadrature Amplitude Modulation (QAM) scheme. To focus on the events happening within one symbol time

January 20, 2022 Wireless/SDR

Least Mean Square (LMS) Equalizer – A Tutorial

The LMS algorithm was first proposed by Bernard Widrow (a professor at Stanford University) and his PhD student Ted Hoff (the architect of the first microprocessor) in the 1960s. Due to its simplicity and robustness, it has been the most widely used adaptive filtering algorithm in real applications. An LMS equalizer in communication system design is just one of those beautiful examples and its other applications include noise and echo cancellation, beamforming, neural networks and so on. Background The wireless channel is a source of severe distortion in the received (Rx) signal and our main task is to remove the