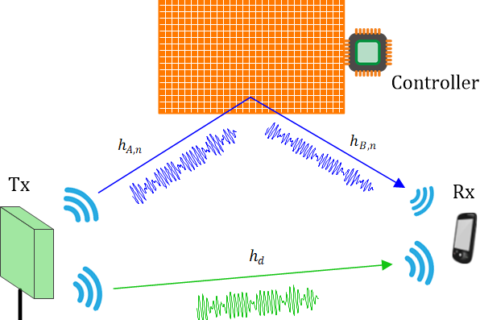
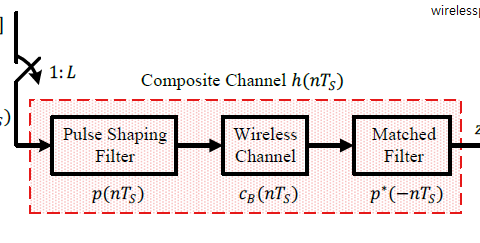
We discussed the idea of fading in wireless channels in a previous article. To understand different types of fading in the context of time variations, refer to the figure below that shows a multipath channel.

Slow Fading
A slow motion scenario is illustrated in the figure below where three multipath components are arriving with Doppler shifts $F_{D,i}$ from the carrier frequency. In this scenario, the magnitudes of $F_{D,i}$ are small and hence observe very little spreading of the cumulative spectrum.

This can be understood by recalling that when two sinusoids with two different frequencies $F_1$ and $F_2$ are added, the resulting signal contains both a sum frequency $F_2+F_1$ and a difference frequency $F_2-F_1$. The envelope of the signal arising from this summation of two sinusoids is given by the difference frequency $F_2-F_1$. When this difference is small, it takes a long time for the envelope to go from one zero to the next and the channel amplitude can be taken as a constant for a large number of symbols. The above figure reveals that the signal bandwidth $B_{\text{QAM}}$ plays a central role in determining how much effect the Doppler spread has on the Rx output. As long as the largest Doppler frequency difference is still a fraction of the signal bandwidth,
\begin{equation*}
|F_{D,\text{max}}-F_{D,\text{min}}| ~<<~ B_{\text{QAM}}
\end{equation*}
as illustrated in the above figure, the motion effects are minimal and the signal undergoes time flat or slow fading.
In time domain, a channel is time flat if it is changing very slowly with respect to the symbol rate $1/T_M$, i.e., the coherence time is much larger than the symbol time $T_M$. As a consequence, the Rx sees an almost constant channel response without any significant variations for a large number of symbols as illustrated in the figure below.

Next, we explore the topic of fast fading.
Fast Fading
A fast motion scenario is illustrated in the figure below where three multipath components are arriving with Doppler shifts $F_{D,i}$ around the carrier frequency. In this scenario, the magnitudes of $F_{D,i}$ are large causing a significant spreading of the cumulative spectrum.
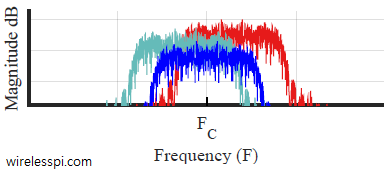
Again, the difference between the frequencies of two sinusoids forms the envelope. When this difference is large, the signal envelope exhibiting a short period quickly complete its repetitions and the channel amplitude varies in proportion, even within a symbol time $T_M$ in some cases. We say that the fading rate is fast or time selective.
Notice that the signal envelope, being inversely proportional to the significant Doppler spread, either changes within a symbol time $T_M$ or very few symbols experience the same fade as illustrated in the figure below. We say that the coherence time is less or on the order of a symbol time $T_M$.

As the term selectivity implies, when some symbols of the signal stream are in a deep fade, the rest of the symbols are not and hence we are able to achieve time diversity through this selective behaviour. Sometimes when we experience a deep fade in a voice call, we successfully overcome it by moving slightly from that place. Motion is a kind of diversity!
Designing a Rx for a static channel during a transmission does not seem to be an excessively difficult task. However, when the channel is changing with time, how can a Rx handle this channel that is acting differently on different data symbols? There are three strategies that are discussed in the article here. Finally, you can read how an LMS equalizer can adapt to the variations in the fading channel to recover the transmitted symbols.