DSP Archives | Page 3 of 14

August 1, 2022 DSP

Spectral Shift without any Multiplications

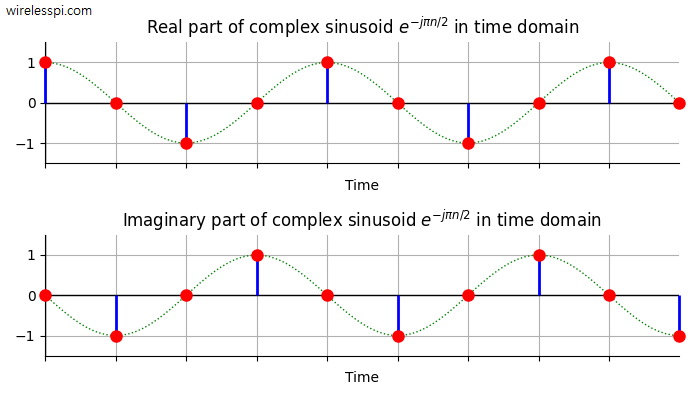
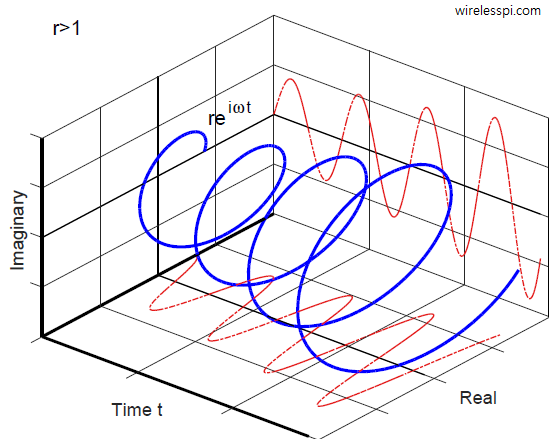
One of the great advantages of Digital Signal Processing (DSP) is an unexpected simplification of operations in seemingly complicated scenarios. See the Cascade Integrator Comb (CIC) filters for how to accomplish the task of sample rate conversion along with filtering with minimal resources. As another example, in wireless communications and many other applications, a frequency translation is often required in which the spectrum of a signal centered at a particular frequency needs to be moved to another frequency. From the properties of Fourier Transform, a shift by frequency $\omega_0=2\pi F_0$ requires sample-by-sample multiplication with a complex sinusoid $e^{j\omega_0 t}$. \[

Reconfigurable Intelligent Surfaces (RIS) concept

July 25, 2022 DSP / Wireless/SDR

Reconfigurable Intelligent Surfaces (RIS) – A Tutorial

For each generation of cellular networks, there is a significant jump in data rates due to the rising demand and novel use cases from emerging applications and associated ecosystems. Some examples in 6G networks are driverless and collaborative transportation, joint communication, localization and sensing, e-health and tactile Internet. Therefore, at the start of each concept-to-deployment cycle, engineers and researchers propose, evaluate and experiment with new ideas, preferably one or two disruptive technologies that can help them meet their targets. For 5G systems, these technologies appeared in the form of a large number of antennas (massive MIMO) and usage of higher

Discrete Fourier Transform (DFT) of a DFT-even sequence

July 11, 2022 DSP

The Beauty of Symmetry in Fourier Transform

In 1978, Fred Harris was a relatively unknown faculty member at the San Diego State University when he published his landmark paper titled On the use of windows for harmonic analysis with the discrete Fourier transform. That paper made him a superstar in DSP community. It presented a brief overview of signal windows and their impact on the detection of harmonic signals in the presence of broad-band noise and nearby harmonic interference. More importantly, he pointed out several common errors in the application of windows when used in the context of Discrete Fourier Transform (DFT). Today I am going to

Individual and cascade frequency responses as well as group delays of the IIR and all-pass filters combination

February 26, 2023 DSP

FIR vs IIR Filters – A Practical Comparison

When it comes to practical applications, digital filter design is one of the most important topics in digital signal processing. Today we discuss a critical question encountered in filter design: how to compare the Finite Impulse Response (FIR) and Infinite Impulse Response (IIR) filters. Since there is no clear winner, answering this question enables a designer to choose the right solution for their product. A brief comparison of FIR vs IIR filters is now explained below. Computational Complexity It is well known that most practical signals are simply sums of sinusoids. This implies that signals with sharp transition in time

March 21, 2022 DSP

A Visualization of Causality and Stability in z-Transform

Most of the books and resources explain the z-Transform as a mathematical concept rather than a signal processing idea. Today I will provide a simple explanation of how the z-Transform helps in determining whether a system is causal and stable. I hope that this visual approach will help my readers learn this concept in a better manner. The z-Transform For a discrete-time signal $h[n]$ (that is the impulse response of a system), the z-Transform is defined as \begin{equation}\label{equation-z-transform} H(z) = \sum _{n=-\infty}^{\infty} h[n]z^{-n} \end{equation} Then, $z$ is a complex number and hence can be written as \[ z = re^{j\omega}