DSP Archives | Page 4 of 14

March 21, 2022 DSP

A Visualization of Causality and Stability in z-Transform

Most of the books and resources explain the z-Transform as a mathematical concept rather than a signal processing idea. Today I will provide a simple explanation of how the z-Transform helps in determining whether a system is causal and stable. I hope that this visual approach will help my readers learn this concept in a better manner. The z-Transform For a discrete-time signal $h[n]$ (that is the impulse response of a system), the z-Transform is defined as \begin{equation}\label{equation-z-transform} H(z) = \sum _{n=-\infty}^{\infty} h[n]z^{-n} \end{equation} Then, $z$ is a complex number and hence can be written as \[ z = re^{j\omega}

March 7, 2022 DSP

DSP and the Humand Mind

It is relatively straightforward to establish the power and potential of human organs. The results are deterministic and not much different than animals. For example, my arm or leg can move only within a certain range and perform a limited number of known tasks. On the other hand, the possibilities with the mind are unlimited. For example, it can plan and execute a drilling mission to dig tunnels in the moons Titan and Europa, all the while sitting here on planet earth! We can say that the mind is the most mysterious organ not only in the human body but

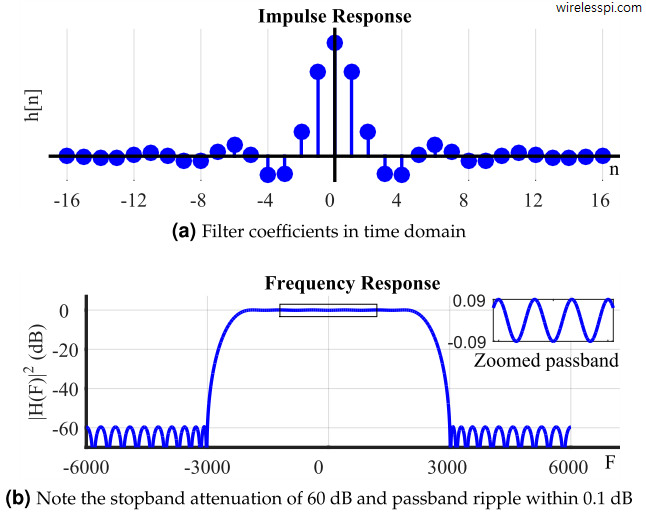
Time and frequency response of a lowpass FIR filter designed with Parks-McClellan algorithm for N=33

August 23, 2022 DSP

Why FIR Filters have Linear Phase

One of the most attractive properties of a Finite Impulse Response (FIR) filter is that a linear phase response is easier to achieve. Not all FIR filters have linear phase though. This is only possible when the coefficients or taps of the filter are symmetric or anti-symmetric around a point. Today I want to describe the reason behind this kind of phase response in an intuitive manner. We have described Finite Impulse Response (FIR) filters before. Moreover, we have also discussed that the Discrete Fourier Transform (DFT) of a signal is complex in general and therefore both magnitude and phase

May 2, 2021 DSP

Convolution and Fourier Transform

One question I am frequently asked is regarding the definition of Fourier Transform. A continuous-time Fourier Transform for time domain signal $x(t)$ is defined as \[ X(\Omega) = \int _{-\infty} ^{\infty} x(t) e^{-j\Omega t} dt \] where $\Omega$ is the continuous frequency. A corresponding definition for discrete-time Fourier Transform for a discrete-time signal $x[n]$ is given by \[ X(e^{j\omega}) = \sum _{n=-\infty} ^{\infty} x[n] e^{-j\omega n} \] where $\omega$ is the discrete frequency related to continuous frequency $\Omega$ through the relation $\omega = \Omega T_S$ if the sample time is denoted by $T_S$. Focusing on the discrete-time Fourier Transform for

July 12, 2021 DSP

Generating Signals and Viewing the Spectrum

One of the most common questions DSP beginners have is how to generate the signals (particularly, sinusoids) and view their spectrum. They have a rough idea what time domain and frequency domain are about but struggle to construct the first few lines of code that open the gates towards a deeper understanding of signals. For this reason, I produce below an Octave (or Matlab) code that you can simply copy and paste to view and modify the results. Keep in mind that the code has been written for an explanation purpose, not conciseness or optimization. As you progress towards developing