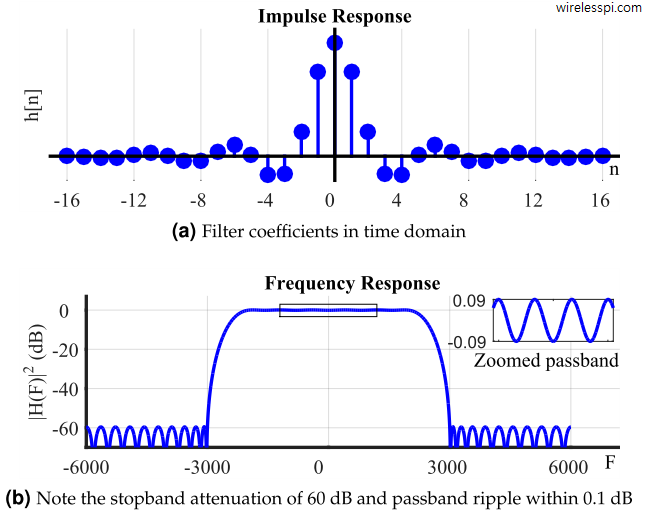
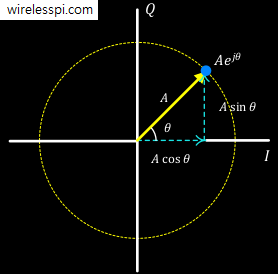
One of the most attractive properties of a Finite Impulse Response (FIR) filter is that a linear phase response is easier to achieve. Not all FIR filters have linear phase though. This is only possible when the coefficients or taps of the filter are symmetric or anti-symmetric around a point. Today I want to describe the reason behind this kind of phase response in an intuitive manner. We have described Finite Impulse Response (FIR) filters before. Moreover, we have also discussed that the Discrete Fourier Transform (DFT) of a signal is complex in general and therefore both magnitude and phase
Continue reading