Pulse Amplitude Modulation (PAM) Archives | Page 2 of 3

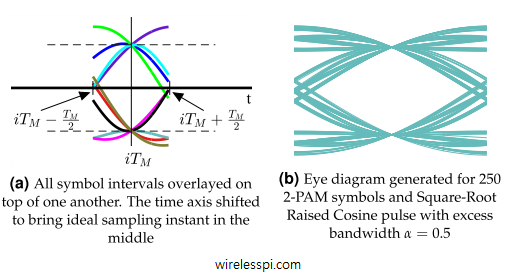
All symbol intervals are overlayed on top of one another and the time axis is shifted to bring ideal sampling instant in the middle. Eye diagram generated for 250 2-PAM symbols and Square-Root Raised Cosine pulse with excess bandwidth 0.5

August 21, 2016 DSP

Tools for Signal Diagnosis

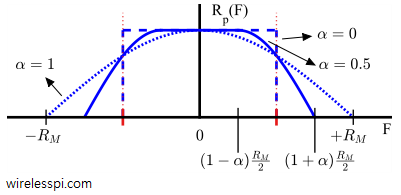
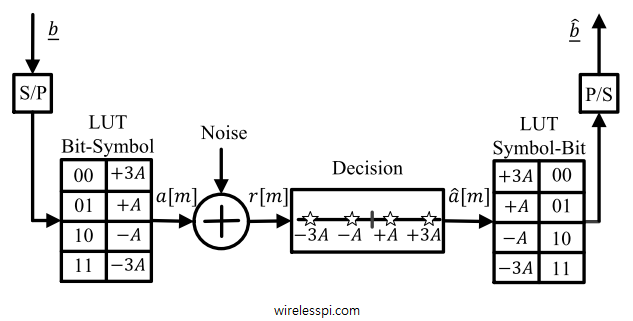
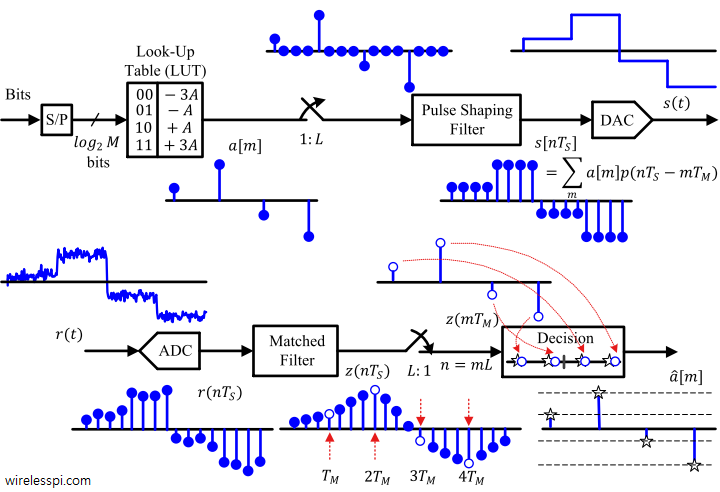
In this article, we will devise some tools that help us diagnose problems with the communication system under study. I like to call them the stethoscopes for a communication system due to the crucial functionality they provide regarding the health of the communication system being analyzed. We discuss three such tools, namely an eye diagram, a transition diagram and a scatter plot below. Eye Diagram An eye diagram is an excellent summary of the signal behaviour in time domain, something analogous to a spectrum in frequency domain. Imagine the samples of the matched filter output taken at a much higher

August 14, 2016 Wireless/SDR

Modulation – From Numbers to Signals

The purpose of digital communications is to send digital data across a channel which can be wireless telephone lines coaxial cable optical fiber Ethernet USB chips on a printed circuit board Considering the examples shown in Figure above, clearly neither a bit sequence nor a symbol sequence can be transmitted on their own through these channels — as they are nothing more than a set of numbers. Therefore, a signal waveform is an appropriate tool that can travel down the channel and carry the required information — just like a train running on its track and carrying the load. For

Square-Root Raised Cosine (SR-RC) spectrum with different excess bandwidths

August 7, 2016 Wireless/SDR

Modulation Bandwidths

From the article on pulse shaping, we can correctly determine the occupied bandwidth for each modulation scheme where the Square-Root Raised Cosine spectrum shows the bandwidth of a Square-Root Raised Cosine pulse shape as $0.5(1+\alpha)R_M$. Also, we have discussed earlier that the spectrum approximately remains the same, provided that there is enough randomness in bit stream and the resulting symbols are equally likely and independent from each other. Therefore, the bandwidth for a PAM modulated signal can be given as \begin{equation}\label{eqCommSystemBWPAM} BW_{\text{PAM}} = 0.5\left(1+\alpha\right)R_M \end{equation} QAM is basically a similar modulation scheme except that it is modulated on a carrier.

Block diagram of a 4 symbol communication system

August 1, 2016 Wireless/SDR

Packing More Bits in One Symbol

Note that digital electronics are constrained to work on only two levels by electronic switches which in the simplest case are either on or off. For many reasons, practical digital communication systems require quite complicated signal processing workload both at the Tx and Rx ends that can be performed only by a device more intelligent than an electronic switch, such as an Application Specific Integrated Circuit (ASIC), Field Programmable Gate Array (FPGA), Digital Signal Processor (DSP) or a General Purpose Processor (GPP). If this intelligent device can differentiate between two signal levels like a switch, it can certainly differentiate between

Block diagram of a pulse amplitude modulator and demodulator

July 24, 2016 Wireless/SDR

Pulse Amplitude Modulation (PAM)

In the article on modulation – from numbers to signals, we said that the Pulse Amplitude Modulation (PAM) is an amplitude scaling of the pulse $p(nT_S)$ according to the symbol value. What happens when this process of scaling the pulse amplitude by symbols is repeated for every symbol during each interval $T_M$? Clearly, a series of bits $b$ (1010 in our initial example) can be transmitted by choosing a rectangular pulse and scaling it with appropriate symbols. \begin{equation*} \begin{aligned} m = 0 \quad b = 1 \quad a[0] = +A \\ m = 1 \quad b = 0 \quad a[1]