This post treats the signals in continuous time which is different than the approach I adopted in my book which deals exclusively in discrete time.
A unit impulse is defined as
\begin{equation*}
\delta (t) = \displaystyle{\lim_{\Delta \to 0}} \begin{cases}
\frac{1}{\Delta} & -\frac{\Delta}{2} < t < +\frac{\Delta}{2} \\
0 & \text{elsewhere}
\end{cases}
\end{equation*}
The result is an impulse with zero width and infinite height, but a consequence of defining it in this way is that the area under the curve is unity.
\begin{equation*}
\text{Area under a rectangle} = \Delta \cdot \frac{1}{\Delta} = 1
\end{equation*}
This is shown in Figure below.

Stated in another way,
\begin{equation*}
\int \limits_{-\infty} ^{+\infty} \delta (t) dt = 1
\end{equation*}
A consequence of this property is that theoretically a particular value of a signal $x(t)$ can be extracted in the following manner.
\begin{equation}\label{eqSiftingProperty}
\int \limits_{-\infty} ^{+\infty} x(t) \delta (t) dt = x(0), \qquad \int \limits_{-\infty} ^{+\infty} x(t) \delta (t-t_0) dt = x(t_0)
\end{equation}
The Fourier Transform of a unit impulse can be derived through the help of Eq \eqref{eqSiftingProperty}).
\begin{equation*}
F\left\{\delta (t) \right\} = \int \limits_{-\infty} ^{+\infty} \delta (t) e^{-j 2\pi f t} dt = e^{-j 2\pi f\ \cdot \ 0} = 1
\end{equation*}
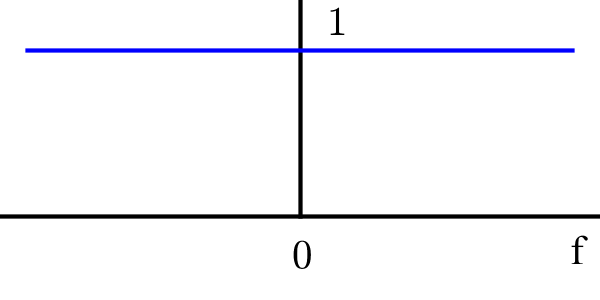
which is a constant for all frequencies from $-\infty$ to $+\infty$. This is shown in Figure below.
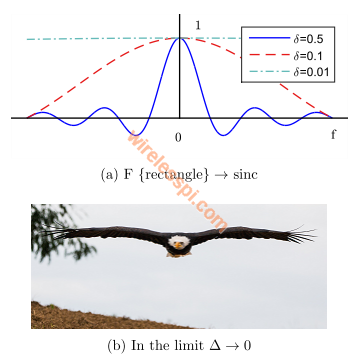
Here, there is a chance of not emphasizing the underlying concept of a unit impulse — a rectangle with width approaching zero. An alternative and beautiful approach in this context is transforming a rectangular signal and taking the limit $\delta \rightarrow 0$. Since the Fourier Transform of a rectangle is a sinc function ($\sin x / x$),
\begin{equation*}
F\left\{\delta (t) \right\} = \displaystyle{\lim_{\Delta \to 0}} \frac{\sin \pi f \delta}{\pi f \delta} \approx \frac{\pi f \delta}{\pi f \delta} = 1
\end{equation*}
where we used the approximation $\sin \theta \approx \theta$ for small $\theta$. With $\delta$ becoming small and approaching zero, the mainlobe of the sinc becomes wider and approaches $\infty$. Imagine an eagle spreading its wings. This illustrated in Figure below and perfectly demonstrates the concept that a signal narrow in time domain has a wide frequency domain representation and vice versa.