The Monty Hall problem is an interesting puzzle loosely based on an American TV game show Let’s Make a Deal hosted by Monty Hall. While the puzzle looked simple, it perplexed some of the brightest mathematical minds in the United States, including the great Paul Erdös who was one of the most prolific mathematicians of the 20th century. This continues to be the case today.
I looked upon a number of references to find the source of confusion in the Monty Hall problem but failed. All I found was different solutions. Therefore, I built one myself with the usual from the ground up philosophy. In this article, I explain the root of this mystery that makes the puzzle so unique.
The Problem
The Monty Hall problem was originally stated and solved by Steve Selvin in a letter to the journal American Statistician in 1975. However, it went ‘viral’ in 1990 when a reader asked the following question in Ask Marilyn column in Parade magazine (the columnist Marilyn vos Savant was known as the world’s smartest woman).
A visual representation of the question is drawn in the figure below.

Assuming that the host always opens a door behind which there is a goat, should you stay with the initially chosen door or should you switch? I invite you to pause here for a moment and come up with your own solution.
.
.
.
The Wrong Answer
Most people reason as follows. Since the car is placed at random behind one of the three doors, and a goat is shown to be behind door 3, now we are left with two doors and two items (a car and a goat). Therefore, the probability of the car behind any of them is 1/2.
This implies that both staying and switching win the car with equal probability. Nevertheless, losing the game after switching hurts more. Therefore, most people decide to stay with the initial choice. As we shortly see, this is the wrong answer.
Marilyn vos Savant responded with the correct solution: “Yes, you should switch. The first door has a 1/3 chance of winning, but the second door has a 2/3 chance.”
And that was when a storm ensued.
A Storm of Letters
After the publication, the magazine received more than 10,000 letters. Around a thousand of them were from PhDs, most of whom said she was wrong. Marilyn must have felt like Harry Potter receiving the barrage of letters under the stairs.

Some of these letters are quoted below (I should have omitted the names of their writers to protect their privacy but they are openly available everywhere).
You blew it, and you blew it big! Since you seem to have difficulty grasping the basic principle at work here, I’ll explain. After the host reveals a goat, you now have a one-in-two chance of being correct. Whether you change your selection or not, the odds are the same. There is enough mathematical illiteracy in this country, and we don’t need the world’s highest IQ propagating more. Shame!
Scott Smith, Ph.D., University of Florida
… If you can admit your error, you will have contributed constructively towards the solution of a deplorable situation. How many irate mathematicians are needed to get you to change your mind?
E. Ray Bobo, Ph.D., Georgetown University
You made a mistake, but look at the positive side. If all those Ph.D.’s were wrong, the country would be in some very serious trouble.
Everett Harman, Ph.D., U.S. Army Research Institute
An error of this magnitude from experts can give us a smug feeling today. But I argue that the statement of the question itself focuses on a corner case that can perplex any human mind. This is a standard trick in the repertoire of psychologists, more on this shortly.
The Correct Solution
Although simple answers are not as mathematically rigorous as the Bayes’ theorem, the easiest I have found is the following.
Referring to the original question, assume that you choose Door 1 at the start.
- The probability of the car behind Door 1 is 1/3 (think of picking a red ball from a bag of 1 red and 2 black balls).
- This means that the probability of the car behind Door 2 and Door 3 as a combination is 2/3.
- After Door 3 is revealed to have a goat behind it, this 2/3 probability refers exclusively to Door 2 now.
- Comparing the probability 1/3 of Door 1 with 2/3 of Door 2, you should switch.
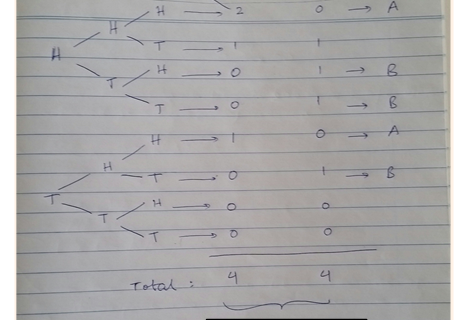
Some people are more comfortable with visual explanations. For this purpose, the figure below depicts the possible scenarios when you have picked Door 1 and the three rows represent the car behind Door 1, 2 and 3, respectively.
- In Stay column, 1 out of 3 scenarios leads to win.
- In Switch column, 2 out of 3 scenarios lead to win.

The above explanation is great but I derived an even simpler one in the context of 100 doors in the Appendix later. For now, let us explore how our minds can be deceived.
Do Maths and Mind Go Along Well?
A human mind is the most amazing machine in the universe. But it evolved in an environment where quick decision making was the difference between life and death. Imagine a rustle in the bushes. Those who immediately ran (an approaching tiger?) had a higher chance of survival as compared to those who gathered more data and took time for analysis before making up their minds.
In today’s modern environment, this kind of decision making leads to faulty conclusions in cases where more observation or attention to detail is required. We have more examples today because some cognitive psychologists develop a special knack for spotting problems that lead to more publications and/or publicity. One popular example is the following.
“A bat and a ball cost \$1.10 in total. The bat costs \$1 more than the ball. How much does the ball cost?”
Most people immediately answer this question as \$0.10. But the correct answer is \$0.05 (since their sum should be \$1.05+\$0.05=\$1.10).
Here, the confusion arises due to the similarity in the following two sentences.
The bat costs \$1 more than the ball.
\$1.10 is \$1 more than \$0.10.
I expect different results when this question is given as follows.
I have seen many other examples but the main pattern is the same: A simple play with words can send the mind in a wrong direction. This leads to the psychologists’ claim that our minds are just not wired to do probability problems well.
In my humble opinion, choosing better words to pose the problem can make a significant difference. After all, it was the human mind that invented the field of probability.
Next, we turn our attention towards the source of this confusion.
Why Monty Hall Problem is Disconcerting
In the statement, there are 3 doors.
- The host never opens the chosen door, say, Door 1.
- The host never opens the door with the car.
- The host opens a SINGLE door behind which there is a goat.
There we have it; a single door is opened. The fact that a single door is left closed does not get our attention!
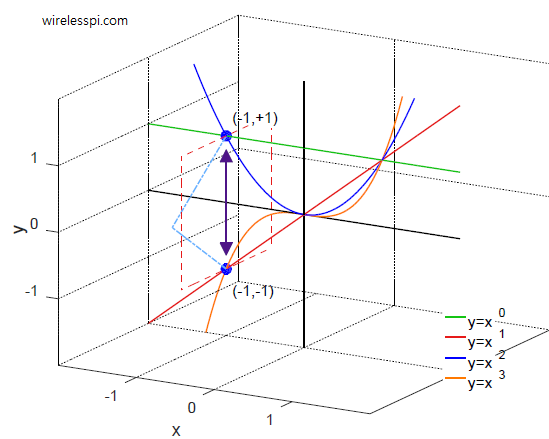
To understand this point, consider the following figure with two branches A and B, both of which have an increasing number of doors.

- In branch A, there is exactly 1 closed door out of 3, 4, 5, $\cdots$ doors.
- In branch B, there is exactly 1 open door out of 3, 4, 5, $\cdots$ doors.
The 3-door scenario is a corner case that lies in both branches! These two branches have different probabilities of win by switching.
For interested readers, the probabilities of win by switching in a general case of $N$ doors for both closed and open doors are derived in the Appendix. This is plotted in the figure below where both branches can be seen as intersecting at 3 doors.

Most people who disagreed with the correct solution gave their answer as 1/2 because there are two doors left closed (1 and 2) in the original question statement. Extending the same idea, we can write a ‘common sensical’ answer as
\[
P(\text{common sense}) = \frac{1}{N-1}
\]
As seen in the Appendix, the win probability in lower branch B with 1 open door readily conforms to intuition. The figure below plots this value with the above common sensical answer which can be seen as quite close.

Clearly, people can be mistaken in part due to the above graph. Read the statement of the original question: “… and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat”. The statement refers to opening only one door (branch B in the above figure), although the host is keeping only one door closed (branch A in the above figure) in the standard solutions!
Conclusion
If a problem misleads a large number of people, it is usually an indicator of a play with words, a corner case or something similar. Although ingenuity of a human mind knows no bounds, it is still good to stay humble.
Appendix
Let us derive the probabilities of a win by switching in both 1 closed door and 1 open door scenarios.
1 Closed Door
Focusing on branch A, imagine a 100 such doors and the following simpler reasoning.
- The probability of a goat behind Door 1 is 99/100 (think of picking a black ball from a bag of 1 red and 99 black balls).
- After Monty reveals all the other goats by opening 98 doors, the only closed door should have the car with the same 99/100 probability.
In words, the probability of a wrong door chosen is very high. When the host opens all other doors except the one with the car, that right door now has the same probability of winning.
For $N$ doors, since the chosen door has a probability $1/N$ for the car and all other doors are opened by Monty Hall, the probability of a win by switching is given by
\[
P(\text{win by switching}) = \frac{N-1}{N}
\]
In the limiting case for a large $N$, we get
\[
P(\text{win by switching}) = \lim_{N\rightarrow \infty}\left(1-\frac{1}{N}\right) \rightarrow 1
\]
Switching leads to an increasingly higher chance of win.
1 Open Door
First consider 4 doors just for fun. All the possible scenarios and their probabilities are given in the figure below if Door 1 is chosen.

Traversing all the branches, the probability of a win by switching is
\[
P(\text{win by switching}) = 6\cdot \frac{1}{16} = \frac{3}{8} = 0.375
\]
which is shown in the following table along with other probabilities.
| Stay | Switch | |
|---|---|---|
| Win | $\frac{1}{4}$ | $\frac{3}{8}$ |
| Lose | $1-\frac{1}{4}$=$\frac{3}{4}$ | $1-\frac{3}{8}$=$\frac{5}{8}$ |
For a general scenario of $N$ doors, this probability can be computed as follows.
- You chose a goat in the first choice which has a probability $(N-1)/N$.
- You are lucky to choose a car after switching. Leaving the first chosen door and the open door, this probability is $1/(N-2)$.
Here, we have excluded the probability of Monty choosing a door for simplification (the final answer is still the same). Therefore, the probability of a win by switching can be written as
\[
P(\text{win by switching}) = \frac{N-1}{N}\frac{1}{(N-2)} = \frac{N-1}{N(N-2)}
\]
which gets closer to $1/N$ for large $N$ and hence ultimately goes to zero. This results in the series given by
\[
P(\text{win by switching}) = \frac{2}{3}, \frac{3}{8}, \frac{4}{15}, \cdots \quad \rightarrow \quad 0
\]
Switching is still better for an open door but with quickly diminishing returns.


Great article Qasim. I have (not so great) memories of discussing this at length with my engineer father who was convinced it would not make a difference.
Oh Dan, you reminded me of my own episode. A similar puzzle once got our attention when I was 20 years old. I had a very long argument with my father and uncle, both of whom were defending their wrong answer. I should have been humble, but unfortunately I was arrogant. Not a good memory.
Since then, I have tried to adopt this habit of admitting my ignorance and saving the person when an argument comes to that. To be honest, I am saving my own self by doing that because the younger generation is 10x more knowledgeable these days. My 10-year-old son defeats me in chess despite my best efforts (I’m not a bad player) and I expect some mercy from him when he is 20 🙂
Hi Quasim,
The logical brain assumes 50/50 and this would be correct if Monty was choosing one of the doors randomly with no knowledge of what lies behind them.
If Monty’s choice was random then 1/3rd of the time he would select the car and given the choice the contestant would always switch to claim the car so switching delivers 100% success 1/3rd of the time.
For the remaining 2/3rds of the time Monty would select a goat and switching would be successful 50% of the time – 50% x 2/3rds is 1/3rd.
Adding the two outcomes together proves that switching works 2/3rds of the time.
Of course in the game Monty always selects a goat and is not acting randomly. This is why the odds from switching logically seem too high, people forget that Monty cannot reveal the car and offer the switch as that would ruin the game show!
I hope this helps all those who cannot understand why 50/50 is the wrong answer.
Chris
Hi Chris,
Thanks for your explanation. Just for clarity: it seems that your first two sentences are contradicting each other.
It would be great if you explain the apparent contradiction for readers’ clarification. Thanks
Hi Qasim,
Monty can pick from two doors. If he picks randomly and the outcome is the goat then following that event the odds of winning from either switching or staying are genuinely 50/50. This is what the logical brain thinks is happening so 50/50 seems like the obvious answer.
In fact Monty is always picking the goat and not behaving randomly and it is this action that is increasing the odds to 2/3rds. By selecting the goat every time Monty is effectively giving you two doors and two chances to win hence the odds improve to 2/3rds.
Chris
Yes, this one is much clearer to understand for any reader. Thank you.
Read ‘game show problem’, vixra.org 2503.0072
This problem in logic has received more attention than it deserves!