Noise is usually considered the main enemy in all DSP applications. As David Tse once said: “Noise is the reason for our existence (communication engineers)!” This short article briefly describes why noise sometimes plays a positive role, e.g., in the context of analog-to-digital conversion when the signal is very weak.
Introduction
Noise is the enemy to be conquered, particularly in communications and radar systems. In a noise-limited regime, we hit a performance brick wall due to the presence of noise. Think of parameter estimation in which the primary criteria is to establish a certain performance against a target signal-to-noise ratio.
In this article, we will investigate one of its underappreciated advantages, specifically in a case when the signal of interest is extremely weak.
Noiseless Signal and Quantization Operation
Let us consider a sinusoidal signal and its 2-bit quantized form. The upper plot in the below figure shows the signal and its quantized form in discrete-time domain. The sinusoid amplitude is very close to 1 and the signal falls to only 3 out of 4 levels. It is clear that the quantized form looks like a square-wave at such a low resolution, which implies an introduction of extra frequency components, known as harmonics.

The lower subplot above shows the frequency response of the signal and its quantized form. We see the DFT of the discrete signal in blue and the quantized signal in red. Note the drop in the amplitude of the sinusoidal signal in red. The distortion caused by quantization process introduced new frequencies in the signal that can be cleaned up by filtering the harmonics out. Quantization is therefore a non-linear operation that is essential for DSP operations.
Weak Noiseless Signal and Quantization Operation
Next consider a weak noiseless signal which is below the lowest quantization level. The signal will only be quantized as only one level which means that there is no information in the signal, see the figure below. The resulting spectrum is clearly all zeros.

We find next how noise plays a beneficial role in such a situation.
Noise Advantage
In general, if the signal is already weak, we would never think of adding noise to it to avoid worsening the situation. However, let us see what happens if we add enough noise to allow the resulting noisy signal to trigger multiple quantization levels. As it happens, the resulting quantized signal surprisingly preserves the sinusoid. Such a discrete-time domain signal and its quantized levels are shown in the figure below.

The sinusoidal signal has the same power as the figure before. However, if we look at the spectrum in the bottom subplot, we can clearly see the peak of the noisy sinusoid at the corresponding frequency. Once quantized, post-filtering can be used to clean the time domain signal even further.
This idea relates to the Buridan’s Donkey. Named after the French philosopher Jean Buridan, this philosophical paradox deals with the free will of an organism.
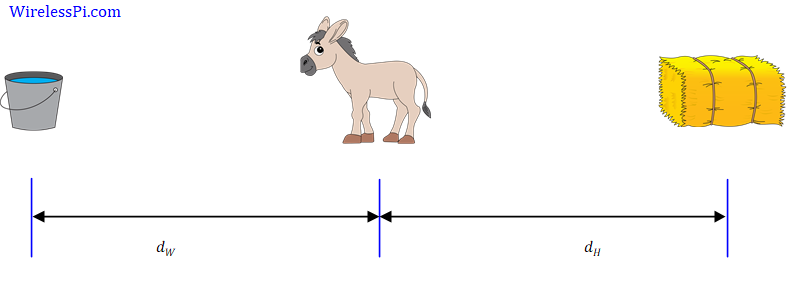
Assume a hypothetical situation where a donkey, who is equally hungry and thirsty, finds itself at an equal distance from a stack of hay and a pail of water.
\[
d_H = d_W
\]
A purely rational donkey would die of both hunger and thirst, unable to decide whether to pursue the hay or water first. A little bit of noise is enough to move the donkey in either direction and enable it to eat and drink in any order, thus saving its life. This is similar to what happens during quantization. A little bit of noise, on average positive half of the time and negative for half of the time, is enough to push the signal values towards the quantization region of the next levels.
Another example is the well-known fact among the investors: Volatility does result in market crashes but is also helps bad investment decisions!
How is This Useful?
This was a toy example of a scenario that happens quite frequently. In practice, noise is exploited in a technique called dithering. It is the process of adding noise to the signal to randomize the quantization effects.
In analog-to-digital (ADC) converters and Direct Digital Synthesizers (DDS), dithering is used to reduce the effects of harmonics generated due to the quantization errors. We saw in the above example that quantization produces harmonics. The undesired effect of harmonics is the inability to differentiate a weak signal from a strong signal since the weaker signal will be inseparable from the harmonic of the stronger signal. Adding a small noise to the signal before ADC can alleviate this problem.
The effect of dithering can be understood better in a visual manner since it is also used in image processing. Dithering allows to capture the features of a grey scale image in a binary image! In the figure below, the original image is on the left, its black and white version with binary thresholding in the middle and the dithered image on the right. We see how dithering allows us to see the features that were removed by the quantization effect in the middle figure.

Finally, in many applications such as Global Positioning System (GPS), we receive a very weak signal that is buried under the noise, i.e., the signal-to-noise ratio (SNR) is negative. This implies that when we quantize the signal, we are actually only quantizing the noise! However, as we saw in our example, if the underlying signal is known, we can always recover it by techniques like correlation, provided that we are able to correlate long enough. Think about the signal we are receiving from Voyager I! How do you think we are able to read the message it is sending?