Interpreting Time Domain Derivative in Frequency Domain

Although this article explains the concepts in terms of mathematical constants e and j as well as integration, my book on SDR steers clear of the complex notation and integrals to describe the underlying concepts from the ground up to an advanced level.

One of the properties of Fourier Transform is that the derivative of a signal in time domain gets translated to multiplication of the signal spectrum by $j2\pi f$ in frequency domain. This property is usually derived as follows.

For a signal $s(t)$ with Fourier Transform $S(f)$
\begin{equation*}
s(t) = \frac{1}{2\pi}\int \limits _{-\infty}^{+\infty} S(f) e^{j2\pi ft}df,
\end{equation*}
we have
\begin{align*}
\frac{d}{dt} s(t) &= \frac{1}{2\pi}\int \limits_{-\infty}^{+\infty}S(f) j2\pi f e^{j2\pi ft}df\\
&= \frac{1}{2\pi}\int \limits_{-\infty}^{+\infty}\bigg\{j2\pi f S(f)\bigg\} e^{j2\pi ft}df
\end{align*}
which is the inverse Fourier Transform of $j2\pi f S(f)$.

Now we want to understand this relation one level deeper, i.e., the reason behind the factor $j2\pi f$? There are two parts of this expression: one is $j$ and the other is $2\pi f$. We start with $2\pi f$.

Notice from the definition of Fourier Transform that this operation decomposes a signal into a sequence of complex sinusoids with frequencies ranging from $-\infty$ to $+\infty$. This is shown in Figure 1 below.

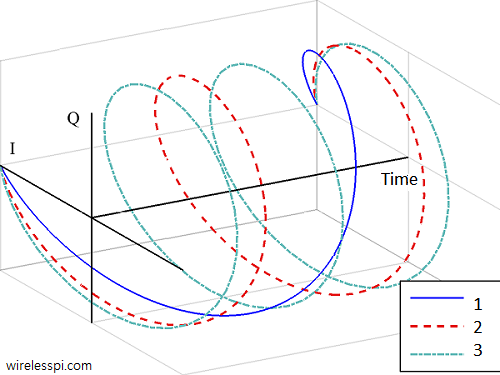
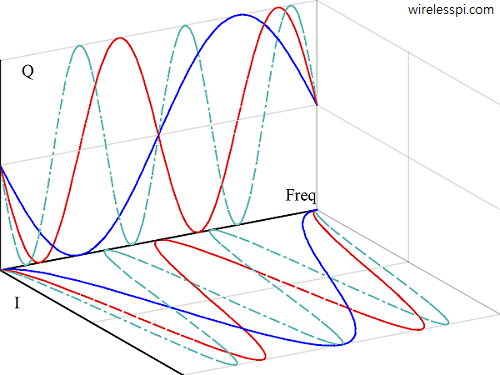
Figure 1: Three complex sinusoids and their decomposition into sines and cosines

By Euler’s formula,
\begin{equation*}
e^{j2\pi ft} = \cos 2\pi ft + j\sin 2\pi ft
\end{equation*}

Naturally, the higher the frequency, the steeper the slope and hence larger the derivative. After all, a derivative is nothing but the slope of the line tangent to the curve at a point. This is where the factor $2\pi f$ comes from (simply put, the derivative of $\cos 2\pi ft$ is $-2\pi f\cdot \sin 2\pi ft$).

The term $j$ is more interesting. The derivative of $\cos 2\pi ft$ is $-2\pi f\cdot \sin 2\pi ft$ while that of $\sin 2\pi ft$ is $2\pi f\cdot \cos 2\pi ft$. So from Euler’s formula and using $j^2=-1$,
\begin{align*}
\frac{d}{dt} e^{j2\pi ft} &= 2\pi f\bigg\{-\sin 2\pi ft + j\cos 2\pi ft \bigg\}\\
&= 2\pi f\cdot j\bigg\{j\sin 2\pi ft + \cos 2\pi ft \bigg\}\\
&= j 2\pi f\bigg\{\cos 2\pi ft + j\sin 2\pi ft\bigg\}\\
\end{align*}

Remembering that $j=e^{j\pi/2}$, the factor $j$ is therefore necessary to rotate $\cos$ and $-\sin$ by their corresponding angles such that we get our basis signals $e^{j2\pi ft}$ back. This results in getting the same signal $S(f)$ at the output with multiplication by $2\pi f$.