We have seen before that diversity implies using two or more statistically independent replicas for the transfer of the same information. This improves the reliability of the received message because nothing can recover the data signal in a deep fade except getting more copies of the same message. Spatial diversity has also been discussed in the context of multiple antenna systems. In this article, we describe how this diversity arising from the presence of multiple antennas can be converted into time or frequency diversity.
- Delay diversity converts spatial diversity into frequency diversity
- Phase-roll diversity converts spatial diversity into time diversity
Space-to-Frequency: Delay Diversity
Multipath in wireless channels is considered as the main villain in typical scenarios. In practice, however, there are certain situations in which we want additional paths of the same signal. For example, when the main path in a deep fade, other signal copies arriving from different paths can help us alleviate the problem. This is where delay diversity comes into the picture.
Assume that in a Multiple-Input Single Output (MISO) system, assume that there are 2 Tx antennas available and only a single Rx antenna as shown in the figure below.

The transmitted symbol at time $m$ is $s[m]$. The signal arriving at the Rx is denoted by $r[m]$ while the flat fading channel gain from Tx antenna $i$ is written as $h_i$. From the above figure, it is evident that the nature adds the signals impinging at the single Rx antenna.
\[
\begin{aligned}
r[m] &= h_1\cdot s[m] + h_2\cdot s[m] = (h_1+h_2)s[m] \\
& \\
&= h\cdot s[m]
\end{aligned}
\]
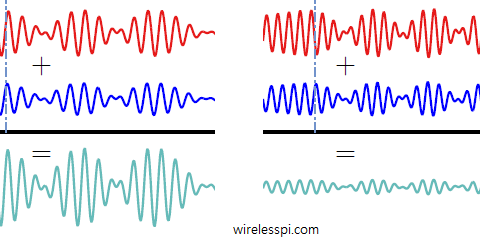
The channel gains $h_1$ and $h_2$ are complex Gaussian random variables with uniformly distributed phases between $0$ and $2\pi$. Their sum also follows a Gaussian distribution with a uniform phase, i.e., $h=h_1+h_2$. This is not much different as a simple Rayleigh fading wireless channel! Once in a fade, there is no way out.
However, if the signal from the second antenna is transmitted after a delay of 1 symbol time, then we have at the Rx
\[
\begin{aligned}
r[m] = h_1\cdot s[m] + h_2\cdot s[m-1]
\end{aligned}
\]
This looks like a two-path channel and the signal arriving at the Rx antenna appears to be from two independent paths with their own respective delays. Consequently, this becomes the well-known frequency selective channel that provides frequency diversity to overcome the signal loss due to fading.
In conclusion, space diversity in a multiple antenna system can be converted into frequency diversity by transmitting a signal from the first antenna and its delayed replica from the second antenna.
Space-to-Time: Phase-Roll Diversity
Phase-roll diversity is not a common terminology but in line with Ref. [1], we continue using the same term here. It helps to change a stationary channel in fade by inducing time variations at the Tx side.
Again, assume that in a Multiple-Input Single Output (MISO) system, assume that there are 2 Tx antennas available and only a single Rx antenna as shown in the figure below.
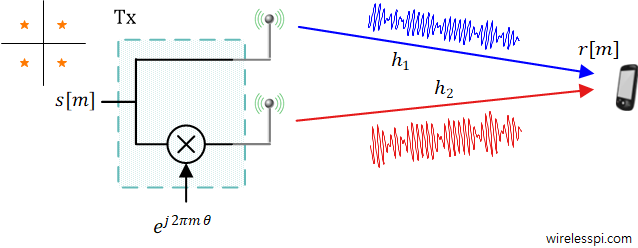
Clearly, the cumulative channel at the Rx antenna is given by
\[
\begin{aligned}
r[m] &= h_1\cdot s[m] + h_2e^{j2\pi m\theta}\cdot s[m]\\
& \\
&= \left(h_1+h_2e^{j2\pi m\theta} \right)\cdot s[m]
\end{aligned}
\]
where $\theta$ is the normalized frequency offset introduced at the second antenna ($|\theta|<1/2$).
Intuitively, it is evident that a time-varying channel at the second antenna introduces time diversity in the overall channel. But it is not clear whether this is independent fading. For this purpose, we can compute the auto-correlation function of the channel response $h[m]=h_1+h_2e^{j2\pi m\theta}$.
Using independent and identically distributed (IID) assumption for $h_1$ and $h_2$, we can derive the correlation at a time interval of $\Delta_m$ as
\[
R[\Delta_m] \propto 1+e^{-j2\pi \Delta_m \theta}
\]
From Euler’s identity,
\[
e^{-j2\pi \Delta_m \theta}=\cos \left(2\pi \Delta_m \theta\right) -j\sin \left(2\pi \Delta_m \theta\right)
\]
Therefore, $R[\Delta_m]$ is zero whenever $\Delta_m\cdot \theta$ is an odd multiple of $1/2$, i.e., $1/2, 3/2, 5/2$ and so on. As a consequence, symbols spaced at $\Delta_m$ interval apart undergo independent fading. Similar to time selective channels, this temporal diversity can be exploited through error correction coding with interleaving.
References
[1] Arogyaswami Paulraj, Dhananjay Gore, and Rohit U. Nabar, Introduction to Space-Time Wireless Communications, Cambridge University Press, 2008.