5G NR standard supports both Frequency Division Duplex (FDD) and Time Division Duplex (TDD) modes in massive MIMO systems. For a reasonably pure estimate, it is necessary to make sure that each pilot transmission in a cell occurs in a vacuum, i.e., free from the interference of other pilots in the same time or frequency. This is achieved through orthogonality or separation of training signals in time or frequency slots. As we see now, simple orthogonality is not enough and new problems emerge due to the interaction among different cells in a network.
Uplink
A set of orthogonal pilots in one cell can also reach the base station antennas of a neighboring cell and interfere with the pilots of that base station. This is the pilot contamination problem where the signal arriving at a base station is a linear combination of pilots from one user in the same cell and another user in a neighboring cell. This is illustrated in the figure below.
Note that it is not necessary that the other user sends the same pilot signal to the base station as the desired user. All the other pilots that are not completely orthogonal to the other pilot will also create additional interference in the uplink during training stage and in the downlink during the data transmission stage as described below.
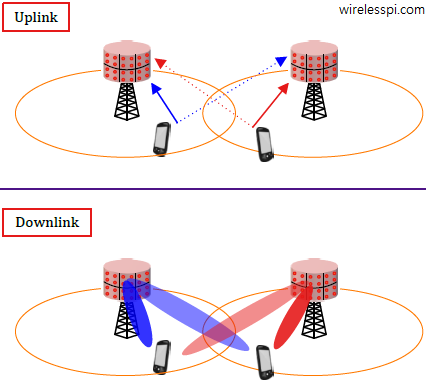
Downlink
During downlink operation, the base station will beamform a signal intended for the original user but it will also unintentionally interfere with the undesired user in the other cell. In the left cell of the above figure, for example, the blue beam is directed towards its cell user but a shadowed blue beam is also arriving at the terminal in the right cell, thus interfering with its original red beam transmission.
Can the pilots be separated in neighboring cells? Yes it is possible but at a huge cost to throughput and efficiency, both of which require as few pilots as possible. Recall the description of a coherence interval which is a time-frequency resource defined by the product of coherence bandwidth $B_C$ and coherence interval $T_C$. The pilots need to be repeated after every coherence interval due to a change in channel conditions. This puts an upper limit on the number of orthogonal pilot sequences. The following remedies for pilot contamination problem can be implemented.
Reuse Factor
A reuse factor determines which cells are assigned the same set of pilots. For example, the figure below shows a reuse factor of 1 at the top. This means that the same set of orthogonal pilots are being used in every cell of the network. This creates problems of interference as demonstrated before. On the other hand, the bottom part of the figure shows a reuse factor of 3 where only the cells of the same color employ the same set of pilots. Clearly, by creating separation between transmissions at the same time-frequency resource, the pilot contamination can be reduced (but cannot be completely eliminated). An even higher reuse factor (e.g., 7) can separate the interfering signals thus creating a larger buffer between cells.

Blind Estimation
There has been a lot of research on blind channel estimation techniques for the past several decades. Blind algorithms estimate the parameter from the signal statistics without any pilot or training from the Tx side. Applications of these techniques can enable a higher throughput network with no transmission tax paid in the form of known training. The drawbacks are the worse quality of the estimate and a longer time to acquire them. A common theme in infrastructure based networks, including 5G, is to insert training at regular intervals/subcarriers for continuous channel estimation and tracking. At this time, this trend seems to continue except in some special circumstances.