Now we turn out attention towards a topic that causes a lot of confusion for communications and DSP learners: what is the difference between a matched filter and a correlator in a communications receiver?
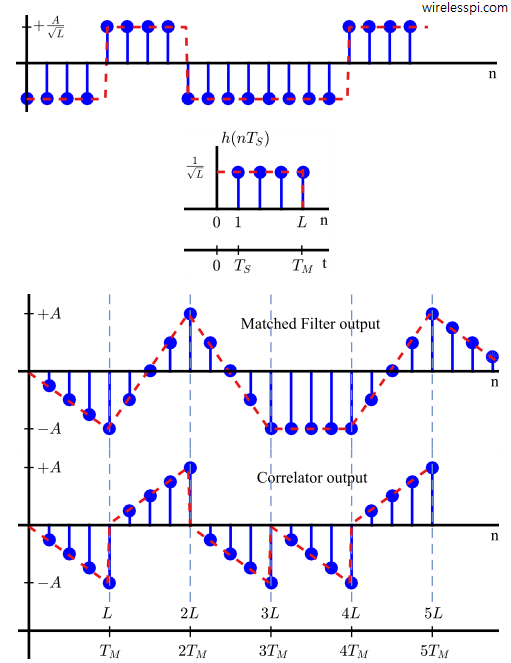
Let us start with the definition of a correlator: A correlator is a device that performs correlation of a received signal with its template within a given window of time. In our context, that window of time is the symbol duration, $T_M$. So a correlator performs the following operations.
- It takes this sample-by-sample product and sums them together.
- Next, it samples the output of this accumulation at the optimal instant $T_M$.
- Finally, it resets itself at each sampling instant $T_M$, i.e., it starts computing the correlation again from zero for the next symbol. This is shown in the figure below.
However, we derived the concept of matched filter in the post on demodulation starting with the definition of correlation as well!
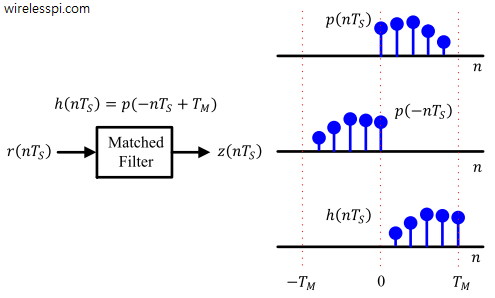
The matched filter, on the other hand, is just a filter that keeps convolving the input signal with the time reversed template while supplying the output at each multiple of $T_M$. Due to this reason, operating at $L$ samples/symbol, both the matched filter and the correlator generate the same output at $L^{th}$ sample but different outputs for the remaining $L-1$ samples (that were going to be discarded anyway). This is plotted in the figure below.
During the days when most of the signal processing was implemented in analog domain, the design of correlator only required an analog mixer (multiplication) and an integrator (summation), the output of which could be sampled at multiples of $T_M$. On the other hand, the matched filter looks simpler in a way that the input enters the system and produces the correlation functionality at the output. However, it is much harder to design an analog filter whose impulse response is some complicated pulse shape (we see the examples of better pulse shapes than a rectangular one in pulse shaping filter). Hence, the correlator receiver was the preferred choice.
After the great advancement in computational power, most of the analog circuits capable of performing analog signal processing (e.g., by using resistors, capacitors, inductors, op amps and so on — basically physics and devices) have been replaced by powerful digital processors that can perform the necessary number crunching (basically algorithms run by computer programs) at a much better price vs performance point. Now, design and implementation of matched filters for any kind of applications is much more convenient, requires less bookkeeping and combines efficiently with other receiver blocks such as synchronizers and equalizers (sometimes I wonder how amazing our world looked like if a revolution like scaling down of a transistor size would have occurred in mechanical world as well).
To conclude, the matched filter computes true correlation of the received signal with the template signal for the duration of the whole symbol sequence, while the correlator resets itself to zero every symbol time.

thanks