Measuring the performance of a digital communication system is not a straightforward task as different impairments have different impacts on the final bit error rate. Error Vector Magnitude (EVM) is a useful metric that helps gauge the impact of all impairments simultaneously from a single value.
A Single Modulation Symbol
We start with observing a single modulation point at the receive end. Once we establish the baseline error in this scenario, we will combine the effect of all such symbol points into a single number.
Assume that a modulation symbol S is represented by a blue constellation point in the figure below. After the transmission, reception and all the changes that it undergoes between the two devices, it is mapped on the red dot as the representative sample of that symbol (see the derivation here for details).
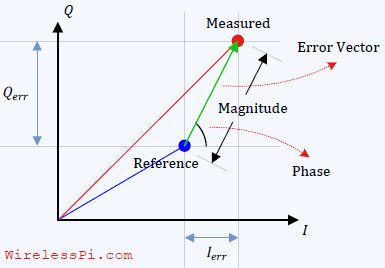
From the figure, it is evident that the error vector is produced by joining the reference symbol with the received sample. This error vector can be broken down into respective $I$ and $Q$ components. The magnitude of this vector is then given by
\[
\text{Magnitude} = \sqrt{I_{\text{err}}^2+Q_{\text{err}}^2}
\]
In the absence of any other received symbols, this value would also have been the EVM if it was also normalized.
\[
\text{EVM} = \frac{\text{Magnitude}}{\text{Normalization Reference}}
\]
Normalization can be done with either the most distant point of the constellation from the origin (the maximum) or the Root Mean Square (RMS) level of the constellation points themselves.
Multiple Modulation Symbols
In reality, one modulation symbol is not sent and the mapped points at the Rx equal the number of modulation symbols sent. Once that happens, the EVM cannot be simply given by the formula mentioned before. Instead, the contributions from all received symbols need to be included and normalized. This is a situation illustrated in the figure below.

The EVM in this case is given by
\[
\text{EVM} = \frac{\sqrt{\frac{1}{N} \sum _{n=0}^{N-1} I_{\text{err}}^2+Q_{\text{err}}^2}}{\text{Normalization Reference}}
\]
where $N$ is the total number of symbols. This can also be converted into a percentage by multiplying the above expression by 100.
Comments
A few comments are now in order.
- Since a number of impairments affect the Tx/Rx process, the beauty of EVM is that it combines the effect of all such impairments into a single value that can be analyzed with relative ease.
- One might think that a lower EVM implies a lower Bit Error Rate (BER) that is true to some extent. The closer the received symbols are to the constellation points, the lower the BER. However, this is only true for small levels of noise. With higher levels of distortion, the demodulated points may get pulled towards other incorrect constellation symbols across the boundaries. In conclusion, while the BER depends on the EVM, the relationship is not linear.
- Major factors impacting the EVM are thermal noise, phase noise and intermodulation products.